有理数是什么？

有理数是什么？

1.3有理数的大小

学习目标：1.会利用绝对值比较两个负数的大小；｜2.掌握任意两个有理数大小的比较法则；｜ 3.通过有理数大小比较的探索过程，培养自己的逻辑推理能力.｜学习重点：会比较任意两个有理数大小.｜学习难点：利用绝对值比较两个负数的大小.｜☆ 预习导航 ☆｜一、链接：（1）数轴上不同的两个点表示的数，右边点表示的数总比 数大；｜（2）负数小于零, 零小于正数， 负数小于正数.｜二、导读：完成以下问题：｜1.在数轴上分别表示下列各数，并比较它们的大小：｜① -3与2 ② -2.4与-2.5 ③ -1与-0.5 ④ -与-0.7｜2、求出上题中各对数的绝对值，并比较它们的大小；｜3、做过上面两题后，你发现了什么规律？｜ ｜三、盘点：｜1、两个负数比较大小，绝对值大的反而小.｜2、两个有理数的大小比较，一般地有：｜①比较两个负数的大小又多了一种方法，即：两个负数，绝对值大的反而小.｜②异号的两数比较大小，要考虑它们的正负；同号两数比较大小，要考虑先比较它们的绝对值.｜③在数轴上表示有理数，它们从左到右的顺序也就是从小到大的顺序，即：左边的数总比右边的数要小.｜☆ 合作探究 ☆｜1、比较下列每组数的大小：｜（1）-2.5与-2.6； （2）－2与－︱－2．3︱．｜2、写出比-4大的所有负整数，并计算它们的绝对值的和.｜3、已知a＞0,b＜0,且∣b∣＜|a|，试比较a、-a、b、-b的大小？｜☆ 达标检测 ☆｜1.比较下列各组数

有理数的概念是什么

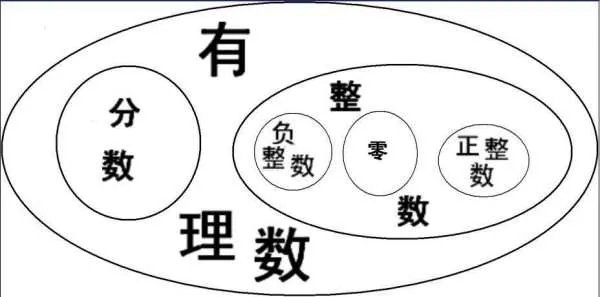
有理数是一个整数a和一个正整数b的比，例如3/8，通则为a/b。0也是有理数。有理数是整数和分数的集合，整数也可看做是分母为一的分数。有理数的小数部分是有限或为无限循环的数。不是有理数的实数称为无理数，即无理数的小数部分是无限不循环的数。

有理数集可以用大写黑正体符号Q代表。但Q并不表示有理数，有理数集与有理数是两个不同的概念。有理数集是元素为全体有理数的集合，而有理数则为有理数集中的所有元素。

扩展资料

有理数的加法运算法则

1、同号两数相加，取与加数相同的符号，并把绝对值相加。

2、异号两数相加，若绝对值相等则互为相反数的两数和为0；若绝对值不相等，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。

3、互为相反数的两数相加得0。

4、一个数同0相加仍得这个数。

5、互为相反数的两个数，可以先相加。

6、符号相同的数可以先相加。

7、分母相同的数可以先相加。

8、几个数相加能得整数的可以先相加。

参考资料来源：

整数可以看作分母为1的分数。正整数、0、负整数、正分数、负分数都可以写成分数的形式，这样的数称为有理数。有理数的小数部分有限或为循环。不是有理数的实数遂称为无理数。

概念

无理数是无限不循环小数。如圆周率、√2（根号2）等。

有理数是由所有分数，整数组成，它们都可以化成有限小数，或无限循环小数。如22/7等。